probability

May 2006

Introduction to Probability

Nomenclature, Symbols, Definitions, Rules
Multiplication symbol ·   (this should appear as a middle dot; however, some browsers may not properly render it)
Complement symbol '   (read as prime)
Union/Or symbol U
Intersection/And symbol ∩   (this should appear as an inverted U; however, some browsers may not properly render it)
Conditional probability P(A|B) means the probability of A given B has occurred
Mutually exclusive Events A and B are mutually exclusive if the occurence of A precludes the occurence of B, i.e., if A ∩ B = null.
Independence Events A and B are independent if and only if P(A|B) = P(A) or P(B|A) = P(B)
Complement rule P(A) + P(A') = 1
Complement rule for conditional probabilities P(A|B) + P(A'|B) = 1
Addition rule P(A U B) = P(B U A) = P(A) + P(B) - P(A ∩ B)
Addition rule if A and B are mutually exclusive P(A U B) = P(B U A) = P(A) + P(B)
Multiplication rule P(A ∩ B) = P(B ∩ A) = P(A)·P(B|A) = P(B)·P(A|B)
Multiplication rule if A and B are independent events P(A ∩ B) = P(B ∩ A) = P(A)·P(B)
Intersection of complements P(A' ∩ B') = 1 - P(A U B)
Rule A1 (see appendix below for proof) P(A ∩ B) + P(A' ∩ B) = P(B)

Appendix

Proof that P(A ∩ B) + P(A' ∩ B) = P(B)

Given the multiplication rule:

P(A ∩ B) = P(B)·P(A|B)
P(A' ∩ B) = P(B)·P(A'|B)

Therefore, P(A ∩ B) + P(A' ∩ B)

= P(B)·P(A|B) + P(B)·P(A'|B)
= P(B)·[P(A|B) + P(A'|B)]

From the complement rule

P(A|B) + P(A'|B) = 1

Therefore,

P(A ∩ B) + P(A' ∩ B) = P(B)

Diagramatically, the proof can be shown through a Venn diagram. Note that A' is everything outside of A, so that A' includes part of B, specifically, B less (A ∩ B).

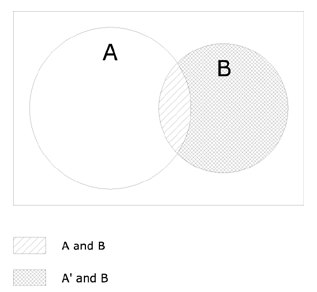
Venn Diagram of P(A and B) + P(A' and B)

As can be seen the union of the two shaded areas--A ∩ B and A' ∩ B--is = B. Therefore, P(A ∩ B) + P(A' ∩ B) = P(B)

References