Introduction to Probability
| Multiplication symbol | · (this should appear as a middle dot; however, some browsers may not properly render it) |
| Complement symbol | ' (read as prime) |
| Union/Or symbol | U |
| Intersection/And symbol | ∩ (this should appear as an inverted U; however, some browsers may not properly render it) |
| Conditional probability | P(A|B) means the probability of A given B has occurred |
| Mutually exclusive | Events A and B are mutually exclusive if the occurence of A precludes the occurence of B, i.e., if A ∩ B = null. |
| Independence | Events A and B are independent if and only if P(A|B) = P(A) or P(B|A) = P(B) |
| Complement rule | P(A) + P(A') = 1 |
| Complement rule for conditional probabilities | P(A|B) + P(A'|B) = 1 |
| Addition rule | P(A U B) = P(B U A) = P(A) + P(B) - P(A ∩ B) |
| Addition rule if A and B are mutually exclusive | P(A U B) = P(B U A) = P(A) + P(B) |
| Multiplication rule | P(A ∩ B) = P(B ∩ A) = P(A)·P(B|A) = P(B)·P(A|B) |
| Multiplication rule if A and B are independent events | P(A ∩ B) = P(B ∩ A) = P(A)·P(B) |
| Intersection of complements | P(A' ∩ B') = 1 - P(A U B) |
| Rule A1 (see appendix below for proof) | P(A ∩ B) + P(A' ∩ B) = P(B) |
Appendix
Proof that P(A ∩ B) + P(A' ∩ B) = P(B)
Given the multiplication rule:
P(A ∩ B) = P(B)·P(A|B)
P(A' ∩ B) = P(B)·P(A'|B)
Therefore, P(A ∩ B) + P(A' ∩ B)
= P(B)·P(A|B) + P(B)·P(A'|B)
= P(B)·[P(A|B) + P(A'|B)]
From the complement rule
P(A|B) + P(A'|B) = 1
Therefore,
P(A ∩ B) + P(A' ∩ B) = P(B)
Diagramatically, the proof can be shown through a Venn diagram. Note that A' is everything outside of A, so that A' includes part of B, specifically, B less (A ∩ B).
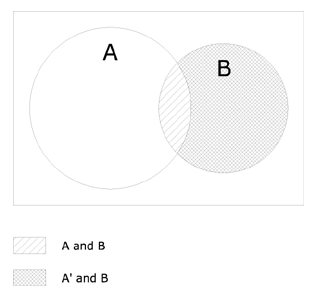
As can be seen the union of the two shaded areas--A ∩ B and A' ∩ B--is = B. Therefore, P(A ∩ B) + P(A' ∩ B) = P(B)
References
- Robert Johnson and Patricia Kuby. 2000. Elementary Statistics, 8th ed. Pacific Grove, CA: Duxbury.
- Ronald E. Walpole. 1982. Introduction to Statistics, 3rd ed. New York: Macmillan.